Nota: este artigo foi desenvolvido em parceria com Ramon Vieira (r_vieira5@hotmail.com) pela disciplina de Mineração de Dados, do curso de Ciência da Computação pela Universidade Federal de São João del-Rei (UFSJ), sob a orientação do Professor Leonardo Rocha (lcrocha@ufsj.edu.br).
INTRODUÇÃO
Com a intensificação do uso de redes sociais por usuários da web, tem sido gerada uma grande quantidade de dados provenientes das interações desses usuários com a rede. Juntamente com o volume de dados, cresce também o interesse na descoberta de conhecimento, sobretudo a respeito de opiniões e tendências disseminadas na rede. Esse interesse impulsiona o desenvolvimento de técnicas de mineração de dados, que permitem extrair conhecimento não trivial em grandes bases de dados.
Entender como os usuários se comportam em uma rede social auxilia em tomadas de decisões, como por exemplo, em estratégias de marketing. Exemplificando, é provavelmente mais eficaz iniciar uma campanha eleitoral a partir de um usuário do qual partem conteúdos amplamente propagados na rede. Outro exemplo de aplicação é em sistemas de recomendação, onde a identificação de grupos de usuários na rede permite a adoção de um método mais efetivo de recomendação de conteúdo.
A fim de verificar o comportamento de uma rede de usuários no Twitter, o trabalho apresentado neste artigo tem por objetivo determinar os usuários mais influentes da rede. Para tal, utilizou-se uma base de dados do Reality Show Big Brother Brasil 2014. O objetivo é aplicar diferentes métricas disponíveis na literatura, que levem em consideração diferentes aspectos da rede. Busca-se também verificar se a opinião disseminada pelos usuários assinalados como mais influentes refletem no resultado do paredão (evento semanal do Reality Show onde o público vota pela saída de um participante da casa).
TRABALHOS RELACIONADOS
Em busca de métricas de influência a serem aplicadas e apoio à construção da metodologia a ser utilizada, fez-se o estudo de alguns artigos científicos que propunham diferentes métodos para identificação de usuários influentes. Foram selecionados aqueles que abordaram cenários mais próximos e apresentaram técnicas mais aplicáveis ao contexto. A seguir, faz-se uma breve descrição desses trabalhos, juntamente com as principais contribuições de cada um deles.
O primeiro trabalho foi desenvolvido por Weng et al. e propõe uma métrica de influência que estende o algoritmo de PageRank. A analogia feita ao algoritmo de PageRank é que, assim como uma página da web, um usuário do Twitter tem alta influência se a soma de influência dos seus seguidores é alta; e sua influência em cada seguidor, por sua vez, é determinada pela quantidade de conteúdo que o seguidor recebe dele. Além disso, o algoritmo acrescenta o peso de uma medida de similaridade entre dois usuários de acordo com os tópicos em que estão interessados. A influência dos usuários é calculada para cada tópico da base, mas pode-se obter uma medida geral de influência, através do montante de influência do usuário. A eficácia do TwitterRank foi demonstrada através de sua correlação com os ranks gerados por outros algoritmos.
O trabalho desenvolvido por Valiati et al. também trata-se de uma extensão do algoritmo PageRank. Entretanto, diferencia-se do primeiro trabalho em duas questões principais: não é topic-sensitive e não leva em consideração a rede de seguidores por questões de eficiência, uma vez que as requisições à API do Twitter são estritamente limitadas. O trabalho modela a rede como um grafo bipartido, que associa usuários a conteúdos propagados por eles, e conteúdo ao usuário que o originou. Dessa forma, utiliza-se uma definição circular de influência e relevância, onde um usuário é influente se dissemina conteúdo relevante, e um conteúdo é relevante se é disseminado por usuários influentes. Intuitivamente, a influência de um usuário pode ser definida pela probabilidade de um randomsurfer(usuário que navega aleatoriamente pelo grafo bipartido) visitar esse usuário. O algoritmo demonstrou sua eficácia no contexto de recomendação de conteúdo, onde se o modelo é capaz de recomendar conteúdo para os usuários de forma acurada, pode-se inferir que a identificação de relevância do conteúdo foi bem sucedida.
Muhammad U. Ilyas e Hayder Radha propõem uma medida de centralidade em redes chamada PCC (Principal Component Centrality), que consiste em considerar a matriz de adjacência do grafo que representa a rede como uma matriz de covariância e partindo dela encontrar os P autovetores mais significativos da matriz. A partir desses autovetores forma-se um auto-espaço e o valor do PCC de cada nó é dado pela norma da distância euclidiana a partir da origem do auto-espaço encontrado. Essa medida de centralidade foi comparada com outra medida bastante utilizada, o EVC (eigenvector centrality), obtendo resultados melhores em relação ao número de comunidades (centros) encontrados. O EVC tem a limitação de se concentrar apenas na maior comunidade, não revelando outras comunidades que podem ter importância significativa. Isso não ocorre com o PCC, conforme comprovado através de testes em uma rede de amigos do Orkut e de uma rede de jogos Fighters Club no Facebook.
Changhyun Lee, Haewoon Kwak, Hosung Park, and Sue Moon propõem um método diferente para medir usuários influentes no Twitter, usando o conceito de leitores efetivos. Um leitor efetivo de um usuário u é um seguidor do usuário u que foi exposto pela primeira vez a um determinado trending topic através de um tweet do usuário u. A influência de um usuário u é medida como o total de leitores efetivos para todos os tweets que o usuário u postou. Usando essa medida de influência, chegou-se ao resultado de que a maioria dos usuários influentes são agências de notícias, que tem uma influência significativa na divulgação de informações. Comparações quantitativas com o método que usa a contagem de número de seguidores mostraram que apenas 34\% de usuários influentes coincidiram, considerando os 1000 mais influentes. O número de influentes comuns, em comparação com o PageRank, foi ainda menor, o que mostra a singularidade desse método frente aos existentes.
TwitterRank
Através de análises de conjunto de dados de usuários do Twitter, foi constatado que 72.4% dos usuários do Twitter segue mais de 80% de seus seguidores, e 80.5% dos usuários tem 80% dos usuários que estão seguindo seguindo-os de volta. De acordo com estudos recentes, essa presença de reciprocidade pode ser explicado pelo fenômeno de homofilia. Com base nessa constatação, foi proposta uma forma de medir a influência de usuários do Twitter com base nessa descoberta.
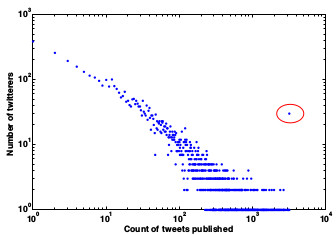 Base de Dados: Usuários de Singapura
Base de Dados: Usuários de Singapura
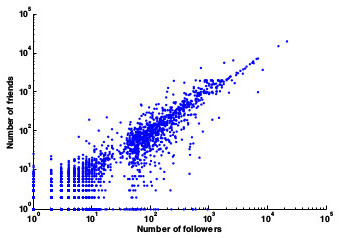
Número de amigos x Número de seguidores
72.4% dos usuários seguem mais de 80% dos seus seguidores e 80.5% dos usuários tem seus amigos seguindo-os de volta. Para responder a questão sobre a presença de homofilia na base, foi necessário fazer as verificações:
- Usuários que se seguem são mais similares do que aqueles que não?
- Identificar o interesse dos usuários (problema: hashtags pouco presentes na base).
Para identificar os interesses, aplica-se uma técnica de aprendizado não-supervisionado: Latent Dirichlet Allocation (LDA). Cada documento D (tweet) está associado com uma distribuição de tópicos T, e cada tópico T está associado a uma distribuição de palavras. A saída é uma matriz DxT, onde D é o número de usuários e T o número de tópicos. Para testar a hipótese:
- Calcular a média da distância de tópicos de cada usuário para seus amigos.
- Mesmo cálculo para o mesmo número de usuários, em que não haja relação entre os usuários.
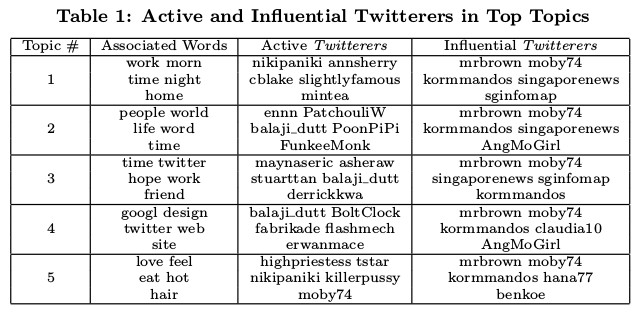 Usuários mais influentes obtidos pelo TwitterRank de acordo com as hashtags
Usuários mais influentes obtidos pelo TwitterRank de acordo com as hashtags
Método de Usuários Influentes -> Conteúdo Relevante
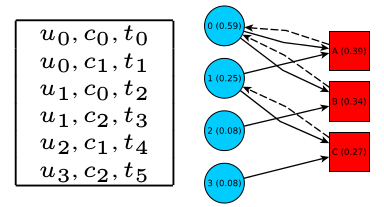 Modelo em grafo bipartido
Modelo em grafo bipartido
O grafo bipartido G(U, C, F, E) pode ser representado por duas matrizes, M e L. A matriz M = (mij) é |U|x|C| e mij = 1/qi. Além disso, L = (lij) é |C| x |U| e lij = 1 se o usuário uj criou o conteúdo ci ou lij = 0, caso contrário.
Cálculo do vetor de Influência/relevância:
pk = pk-1 ML, onde p0 = vetor uniforme
rk = rk-1 LM, onde p0 = vetor uniforme
Esse modelo apresenta dois problemas importantes: a possível presença de usuários dangling e a possível existência de buckets. Nesse caso, a soluçao consiste na adição de mecanismo de amortecimento d. Assim, após o reajuste, o novo modelo é apresentado da seguinte forma (utilizou-se d=0.85, segundo o trabalho de referência):
pk = dpk-1 ML + (1 – d)u
rk = drk-1 LM + (1 – d)u
Após reformular as equações acima algebricamente, a fim de obter-se a forma não recursiva:
p = (1 – d)u(I – dML)-1
r = (1 – d)u(I – dLM)-1
Problema: computação custosa. Solução: aplicar o método das potências para solução aproximada, mas eficiente:

Para a base onde os autores executaram o algoritmo, obteve-se os seguintes resultados:
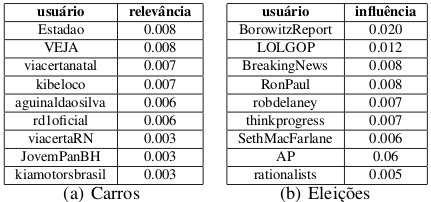
Principal Component Centrality
Para calcular a influência dos usuários, essa métrica utiliza a modelagem da rede de usuários do Twitter como um grafo, e a partir do cálculo de centralidade nesse grafo pode-se estimar o quanto um determinado usuário é influente nessa determinada rede.
Essa métrica é baseada em uma outra métrica bastante difundida no estudo de redes sociais, o EVC (centralidade de autovetor). Para calcular a centralidade de cada nó, o EVC dá uma pontuação a esse nó do grafo em relação aos seus vizinhos. Isso é feito relacionando tanto o número de ligações entre os nós, a robustez entre essas ligações e por fim às centralidades dos nós vizinhos. Para poder encontrar os valores exatos das centralidades, sendo que não pode ser feito calculando a centralidade de cada nó por vez, é utilizando o autovetor principal da matriz de adjacência do grafo.
Essa característica permite que o EVC de um determinado nó, assim como o closeness e o betweenness, forneça uma perspectiva de toda a rede. Cada nó receberá um valor de centralidade que indica o “grau” de conexão ao nó mais central, ou mais dominante. Porém o EVC tem uma característica que pode não ser muito interessante em determinadas bases de dados: é uma métrica que foca somente na maior comunidade de nós centrais, ignorando que existam outras vizinhanças de nós com centralidades menores porém que podem ser igualmente importantes.
Visando obter uma métrica que consiga detectar múltiplas comunidades em um grafo, foi desenvolvida uma métrica nova chamada PCC (Principal Component Centrality). Essa métrica utiliza uma técnica de redução de dimensionalidade chamada PCA na matriz de adjacência do grafo, transformando o espaço vetorial formado pela matriz de adjacência do grafo, em que cada dimensão representa um nó e suas adjacências, em outro espaço vetorial reduzido, no qual se preserve o máximo de informação possível. Após fazer essa redução, calcula-se a centralidade de cada nó como a distância euclidiana entre a origem do espaço vetorial e a projeção do nó nesse espaço reduzido.
Para a escolha de uma dimensão apropriada para a redução, é feito um cálculo de phase angle entre o autovetor do EVC e o vetor de distâncias calculado pelo PCC para uma dimensão d. A dimensão d é escolhida se a variação entre o phase angle para uma dimensão d e uma dimensão d-1 for pequena, indicando que a partir dali os valores do PCC não sofrerão grandes alterações.
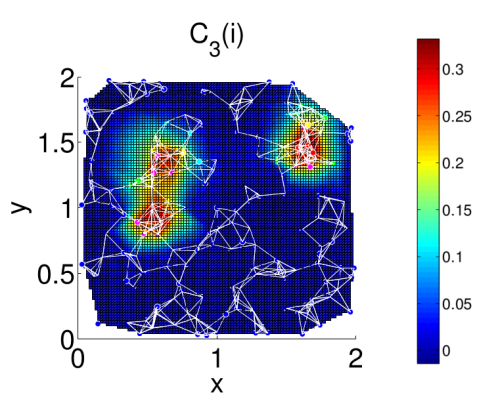 Exemplo de cálculo de centralidade usando o PCC
Exemplo de cálculo de centralidade usando o PCC
Leitores Efetivos
A dinamicidade do Twitter, onde a qualquer momento um usuário ou um grupo de usuários pode causar uma mudança repentina da opinião geral sobre um determinado assunto, faz com que a temporalidade dos posts tenha grande relevancia na identificação de usuários influentes. Porém, muitas das abordagens atualmente utilizadas para essa análise, como o número de seguidores e o PageRank, não utilizam informações temporais para esse fim. De modo a usar essas informações temporais, foi desenvolvida uma métrica chamada Leitores Efetivos.
Ao analisar a maneira como se dá a difusão de informação no Twitter, constatou-se que o número de usuários do Twitter que recebem tweets sobre um determinado trending topic cresce de forma acelerada no início do período de evidência de um determinado trending topic. Em contrapartida, o número de usuários que escrevem tweets sobre esse determinado trending topic apresenta um crescimento muito menor. Conforme o tempo vai passando, o número cumulativo de usuários que recebe tweets se estabiliza, enquanto o número de escritores continua crescendo.
Ao se fazer uma análise mais atenta percebe-se que o número de leitores proporcionalmente ao número de escritores é muito maior no início do período de evidência, decaindo conforme o tempo passa e o número de escritores aumenta. Com base nessa observação, pode-se dizer que um usuário que escreve um determinado conteúdo no início do período é mais influente do que outro que escrever em um período posterior, pois o primeiro atinge muito mais usuários do que o segundo.
Desse modo, pode-se medir a influência através dos chamados leitores efetivos. Um leitor efetivo de um tweet t postado por um usuário u é qualquer usuário f, seguidor de u, que tem contato com um determinado trending topic através do tweet t. Caso f tenha sido exposto a uma determinado trending topic através de tweets de vários usuários a quem segue, o usuário f será o leitor efetivo do tweet do usuário que postou a informação primeiro, de modo que cada usuário seja leitor efetivo de apenas 1 tweet. A influência de cada usuário é calculada como o somatório das influências de todos os tweets postados por aquele usuário.
METODOLOGIA
A seguir é descrita a metodologia utilizada para a formulação do trabalho. Primeiramente foi feito um estudo de como cada métrica funciona, de forma a auxiliar na etapa posterior de implementação. Depois dessa etapa segue o pré-processamento da base de dados utilizada, assim como a construção do grafo posteriormente utilizada para as métricas de Usuários Influentes/Conteúdo Relevante e PCC.
Após essa etapa de pré-processamento, foi feita a implementação das métricas Usuários Influentes/Conteúdo Relevante, PCC e TwitterRank, descritas a seguir. A métrica \textit{Effective Readers} não pôde ser implementada devido a falta de informações relativas aos trending topics na base de tweets que foi utilizada para as análises das demais medidas de centralidade.
Modelagem do grafo
O grafo G = (V, E) foi modelado de forma que, cada elemento de V representa um usuário que gera tweets ou é mencionado em um tweet, e o conjunto E é composto por arestas que indicam uma relação entre um par de usuários, na qual um usuário cita o outro usuário através de um tweet. Para as métricas grau de entrada, \textit{PageRank} e \textit{betweenness}, esse grafo foi modelado como um grafo direcionado. Já para o PCC, o grafo foi modelado de forma não-direcionada. Para a métrica Usuários Influentes / Conteúdo Relevante, o modelo de grafo utilizado foi um grafo bipartido que associa usuários a conteúdos, e foi modelado através de duas matrizes M e L.
Usuários Influentes/Conteúdo Relevante
A implementação foi feita usando duas matrizes: M e L. A matriz M é uma matriz de dimensões |U|x|C|, onde |U| é o número de usuários e |C| a quantidade de conteúdo. Cada linha i da matriz é preenchida com o valor inverso da quantidade de conteúdo propagado pelo usuário i. A matriz L, de dimensões inversas (|C|x|U|) representa a criação de conteúdo por parte dos usuários, onde cada posição (i,j) contém o valor 1 caso o conteúdo i tenha sido originado pelo usuário j, e 0 caso contrário.
Utilizando o método das potências apresentado anteriormente, utilizou-se como Z1 a matriz M e Z2 como a matriz L, uma vez que o objetivo é somente a identificação de usuários influentes. Para o parâmetro k, utilizou-se 10 iterações onde verificou-se que os resultados mantinham-se, alterando somente o valor obtido pela métrica para valores mais precisos. Para o parâmetro de amortização d, utilizou-se o mesmo parâmetro dos autores do artigo (0.85).
Para a base de dados utilizada, foi necessária utilizar artifícios de implementação para contornar o problema de falta de memória. Para a matriz M, foi feita sua representação através de um vetor, uma vez que o valor para cada linha se mantém, e alterou-se os métodos para que esse vetor fosse tratado como uma matriz. Para a matriz L, uma vez que está é esparsa, utilizou-se uma representação por dicionários, onde somente armazena-se as tuplas onde o valor é diferente de 0.
Principal Component Centrality
Para a implementação da métrica de centralidade PCC, o método que foi utilizado para extração de autovalores e autovetores de uma matriz foi o SVD (Singular Value Decomposition), presente na biblioteca Numpy. Esse método consiste em fatorar uma matriz qualquer em três matrizes M = UΣV*,
onde U é uma matriz unitária m x m real ou complexa,Σ é uma matriz retangular diagonal m x n com números reais não-negativos na diagonal, e V* (a conjugada transposta de V) é uma matriz unitária n x n real ou complexa. Ao aplicar o SVD na matriz de adjacência M do grafo G, as matrizes U e Σ contém os valores dos autovetores e dos autovalores, respectivamente. Esses valores foram calculados para cada valor de dimensão d até que o se estabilizasse a partir de uma determinada dimensão n.
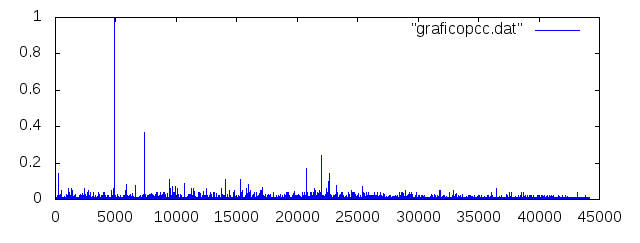
Para que a implementação feita fosse validada, a implementação foi executada para a base de dados do Orkut, uma das bases de dados utilizada na extração de usuários influentes pelos autores que propuseram a métrica. Ao avaliar os resultados, chegou-se a um resultado semelhante, no qual o usuário mais influente detectado foi o usuário 692, e em seguida usuários com ids próximos a 43000, o que validou a utilização do mesmo na utilização em outras bases de dados.
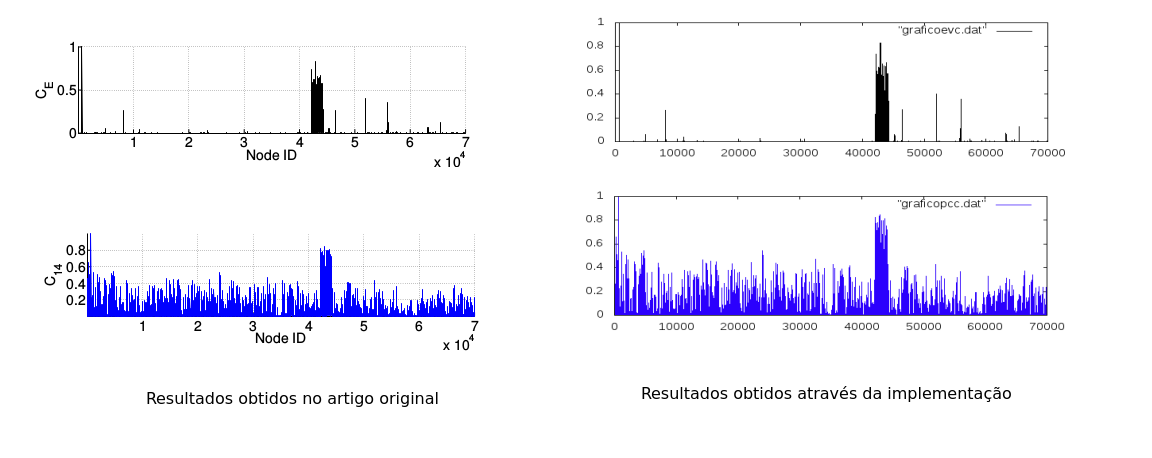 Comparação entre os resultados originais e os obtidos pela nossa implementação
Comparação entre os resultados originais e os obtidos pela nossa implementação
RESULTADOS
| Grau | PageR. | Betweeness | PCC | UFMG | |
| Grau | 1.0 | 0.81 | 0.32 | -0.01 | 0.25 |
| PageR. | 0.81 | 1.0 | 0.18 | -0.05 | 0.10 |
| Betweeness | 0.32 | 0.18 | 1.0 | 0.56 | 0.65 |
| PCC | -0.01 | -0.05 | 0.56 | 1.0 | 0.69 |
| UFMG | 0.25 | 0.10 | 0.65 | 0.69 | 1.0 |
Tabela de Correlação – Base do BBB
| Grau | PageR. | Betweeness | PCC | UFMG | |
| Grau | 1.0 | 0.73 | -0.18 | -0.14 | -0.11 |
| PageR. | 0.73 | 1.0 | 0.05 | 0.03 | 0.007 |
| Betweeness | -0.18 | 0.05 | 1.0 | 0.51 | 0.56 |
| PCC | -0.14 | 0.03 | 0.51 | 1.0 | 0.60 |
| UFMG | -0.11 | 0.007 | 0.56 | 0.60 | 1.0 |
Tabela de Correlação – Base do jogo Argentina x Irã
- Grau de Entrada: @Tropa Clanessa: “#FORAAMANDA VOTEM VOTEM http://t.co/O71znFWeWX“.
- Betweenness e UFMG: @EitaBBB: “@ka up Mutirao no @Portal Clanessa ate o encerramento dos votos, vem participa #ForaAmanda #FicaVanessa http://t.co/tf7Mll9x6v“.
- PageRank: @HugoGloss: “Obaaaaaa! Amandaaaaa foraaaaa!!! Vai fazer propaganda da Koleston, querida #BBB14”.
- PCC: @VAZA03PANACAS: “#FORAAMANAJAAAAAAAA #VAZAAAAAAAAAAMANAJAAAAAAAAA #foraa-manda #BBB14”.
CONCLUSÃO
Por fim, após a aplicação das métricas e análise dos resultados, identificou-se algumas particularidades sobre cada uma dessas métricas:
- Grau de entrada: Métrica simples que geralmente identifica pessoas famosas ou spammers.
- Betweenness: Usuários que são o centro do fluxo de informação. Geralmente fã-clubes ou propagadores de conteúdo.
- PageRank: Altamente correlacionado com o grau de entrada, e portanto, também identifica usuários desse grupo.
- Leitores Efetivos: Identifica agência de notícias e jornais, que têm acesso mais rápido às informações e as divulgam primeiro.
- PCC: Voltado para identificação de comunidades de usuários influentes.
- TwitterRank: Usuários mais influentes de acordo com assunto de interesse.
- UFMG: Identifica usuários comuns, cujo conteúdo é muito repercutido.
Essas particularidades fazem cada métrica mais apropriada em sua devida aplicação. Uma vez que o conceito de influência é subjetivo, devem ser avaliados os aspectos relevantes da aplicação a fim de tomar-se uma decisão acerca da métrica a ser utilizada.
 Home
Home

1 Comentário
Sannytet
11 de dezembro de 2018 at 21:26Nice posts! 🙂
___
Sanny